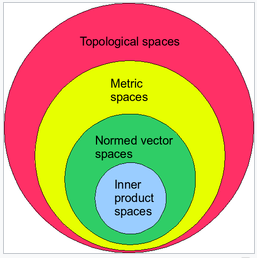
Inner product space

A (real or complex) vector space together with an inner product:

• a non-degenerated

• conjugate-symmetric

• bilinear form,

• which is positive-definite.

In the case of $\mathbb{C}$ it is called a Hermitian inner product. In the case of $\mathbb{R}$ is a scalar product or dot product.

If the associated norm gives rise to a topology such that the space is Cauchy complete then it is called a Hilbert space

Identities

• Pithagoras theorem inner product spaces

• Bessel's inequality

• Cauchy-Schwarz inequality

• ...

Orthonormal basis

They are basis of the vector space which satisfy $\langle e_i,e_j \rangle=\delta_{ij}$.

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es